说明
本文大部分内容翻译自Matrix calculus,部分结合自身的理解。
简单来说,矩阵求导就是分别将各元素进行求导,然后将求导的结果写成矩阵的形式(向量为矩阵特殊形式),根据写成的矩阵的排列方式,又分为分子布局和分母布局。
- 分子布局:行数和分子相同的维度,列数和分母相同的维度。如列向量对列向量的导数为分子各元素分别对分母各元素的导数,然后将结果排列为矩阵,矩阵的行数为分子的行数,矩阵的列数为分母的行数
- 分母布局:行数和分母相同的维度,列数和分子相同的维度。如列向量对列向量的导数为分子各元素分别对分母各元素的导数,然后将结果排列为矩阵,矩阵的行数为分母的行数,矩阵的列数为分子的行数
- 混合布局:向量或者矩阵在分子时采用分子布局,向量或矩阵在分母时采用分母布局。
布局方式详细参见Layout conventions,不同的文章可能使用不同的布局方式,如在深度学习的领域中,如在优化算法中需要计算$\boldsymbol{W}-\alpha\frac{\partial{L}}{\boldsymbol{W}}$时,为了保证维度相容,就采用的是分母布局或混合布局。无需纠结,最终只是在求导结果中相差个转置,其实只要保证求导的结果矩阵维度相容,一般就没有问题,本文采用分子布局。
向量和矩阵之间,矩阵和矩阵之间的导数涉及到三维、四维张量,这里暂不考虑这种导数。
符号说明
我们使用$M(n,m)$表示包含$n$行$m$列的$n*m$实矩阵的空间,该空间中的一般矩阵用粗体大写字母表示,如$\boldsymbol{A,X,Y}$等,
而若该矩阵属于$M(n,1)$,即列向量,则用粗体小写字母表示,如$\boldsymbol{a,x,y}$等,不做特别说明的话,向量默认为列向量,
特别地,$M(1,1)$空间中的元素为标量,用小些斜体字母表示,如$a,x,y$等。
通常使用字母表的前半部分$(a,b,c,\cdots)$用于表示常量,字母表的后半部分$(x,y,z,\cdots)$表示变量。
- 标量$a,b,c,d,e$为常量,标量$u,v$为$x$、$\boldsymbol{x}$或$\boldsymbol{X}$的函数
- 向量$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c},\boldsymbol{d},\boldsymbol{e}$为常向量,向量$\boldsymbol{u},\boldsymbol{v}$为$x$、$\boldsymbol{x}$或$\boldsymbol{X}$的函数
- 矩阵$\boldsymbol{A},\boldsymbol{B},\boldsymbol{C},\boldsymbol{D},\boldsymbol{E}$为常矩阵,矩阵$\boldsymbol{U},\boldsymbol{V}$为$x$、$\boldsymbol{x}$或$\boldsymbol{X}$的函数
矩阵的转置:$\boldsymbol{X}^{\mathrm{T}}$,矩阵的迹:$\text{tr}(\boldsymbol{X})$,矩阵的行列式:$\text{det}(\boldsymbol{X})$或$|\boldsymbol{X}|$,矩阵的范数:$||\boldsymbol{X}||$。
向量求导定义
向量可以看作只有一列的矩阵,是矩阵求导的特殊情况
向量对标量求导定义
向量$\boldsymbol{y}=[y_1,y_2,\cdots,y_m]^{\mathrm{T}}$对标量$x$的导数写成如下形式:
\[\frac{\partial{\boldsymbol{y}}}{\partial{x}} = [\frac{\partial{y_1}}{\partial{x}},\frac{\partial{y_2}}{\partial{x}},\cdots,\frac{\partial{y_m}}{\partial{x}}]^{\mathrm{T}}\]即:
\[(\frac{\partial{\boldsymbol{y}}}{\partial{x}})_i = \frac{\partial{y_i}}{\partial{x}}\]标量对向量求导定义
标量$y$对向量$\boldsymbol{x}^{\textrm{T}}=[x_1,x_2,\cdots,x_n]$对的导数写成如下形式:
\[\frac{\partial{y}}{\partial{\boldsymbol{x}^\textrm{T}}} = [\frac{\partial{y}}{\partial{x_1}},\frac{\partial{y}}{\partial{x_2}},\cdots,\frac{\partial{y}}{\partial{x_n}}]^{\textrm{T}}\]即:
\[(\frac{\partial{y}}{\partial{\boldsymbol{x}^{\textrm{T}}}})_i = \frac{\partial{y}}{\partial{x_i}}\]向量对向量求导定义
向量$\boldsymbol{y}=[y_1,y_2,\cdots,y_m]^{\mathrm{T}}$对向量$\boldsymbol{x}=[x_1,x_2,\cdots,x_n]^{\mathrm{T}}$对的导数写成如下形式:
\[\frac{\partial{\boldsymbol{y}}}{\partial{\boldsymbol{x}}} = \left[ \begin{matrix} \frac{\partial{y_1}}{\partial{x_1}} & \frac{\partial{y_1}}{\partial{x_2}} & \cdots & \frac{\partial{y_1}}{\partial{x_n}} \\ \frac{\partial{y_2}}{\partial{x_1}} &\frac{\partial{y_2}}{\partial{x_2}} & \cdots & \frac{\partial{y_2}}{\partial{x_n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial{y_m}}{\partial{x_1}} &\frac{\partial{y_m}}{\partial{x_2}} & \cdots &\frac{\partial{y_m}}{\partial{x_n}} \\ \end{matrix} \right]\]为$m*n$维矩阵,也叫做雅可比矩阵。即:
\[(\frac{\partial{\boldsymbol{y}}}{\partial{\boldsymbol{x}}})_{ij} = \frac{\partial{y_i}}{\partial{x_j}}\]矩阵求导定义
矩阵对标量求导定义
矩阵$\boldsymbol{Y}$对标量$x$的导数定义如下:
\[\frac{\partial{\boldsymbol{Y}}}{\partial{x}} = \left[ \begin{matrix} \frac{\partial{y_{11}}}{\partial{x}} & \frac{\partial{y_{12}}}{\partial{x}} & \cdots & \frac{\partial{y_{1n}}}{\partial{x}} \\ \frac{\partial{y_{21}}}{\partial{x}} &\frac{\partial{y_{22}}}{\partial{x}} & \cdots & \frac{\partial{y_{2n}}}{\partial{x}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial{y_{m1}}}{\partial{x}} &\frac{\partial{y_{m2}}}{\partial{x}} & \cdots &\frac{\partial{y_{mn}}}{\partial{x}} \\ \end{matrix} \right]\]即:
\[(\frac{\partial{\boldsymbol{Y}}}{\partial{x}})_{ij} = \frac{\partial{y_{ij}}}{\partial{x}}\]标量对矩阵求导定义
标量$y$对矩阵$\boldsymbol{X}$的导数定义如下:
\[\frac{\partial{y}}{\partial{\boldsymbol{X}}} = \left[ \begin{matrix} \frac{\partial{y}}{\partial{x_{11}}} & \frac{\partial{y}}{\partial{x_{21}}} & \cdots & \frac{\partial{y}}{\partial{x_{p1}}} \\ \frac{\partial{y}}{\partial{x_{12}}} &\frac{\partial{y}}{\partial{x_{22}}} & \cdots & \frac{\partial{y}}{\partial{x_{p2}}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial{y}}{\partial{x_{1q}}} &\frac{\partial{y}}{\partial{x_{2q}}} & \cdots &\frac{\partial{y}}{\partial{x_{pq}}} \\ \end{matrix} \right]\]即:
\[(\frac{\partial{y}}{\partial{\boldsymbol{X}}})_{ij} = \frac{\partial{y}}{\partial{x_{ji}}}\]求导法则
在微分、求导过程中,有三条法则非常重要,在矩阵的微分、求导过程中也同样重要。
- 链式法则:如果$y = f(g(x))$,则$y^\prime(x) = f^\prime(g(x))g^\prime(x)$
- 乘积法则:$(fg)^\prime = f^\prime g+fg^\prime$
- 求和法则:$(f+g)^\prime = f^\prime + g^\prime$
求和法则是通用的,由于矩阵乘积不是可交换的,所以乘积法则需要注意顺序。链式法则在矩阵对标量和标量对矩阵求导时不适用(这个情况下,一般使用迹运算)。
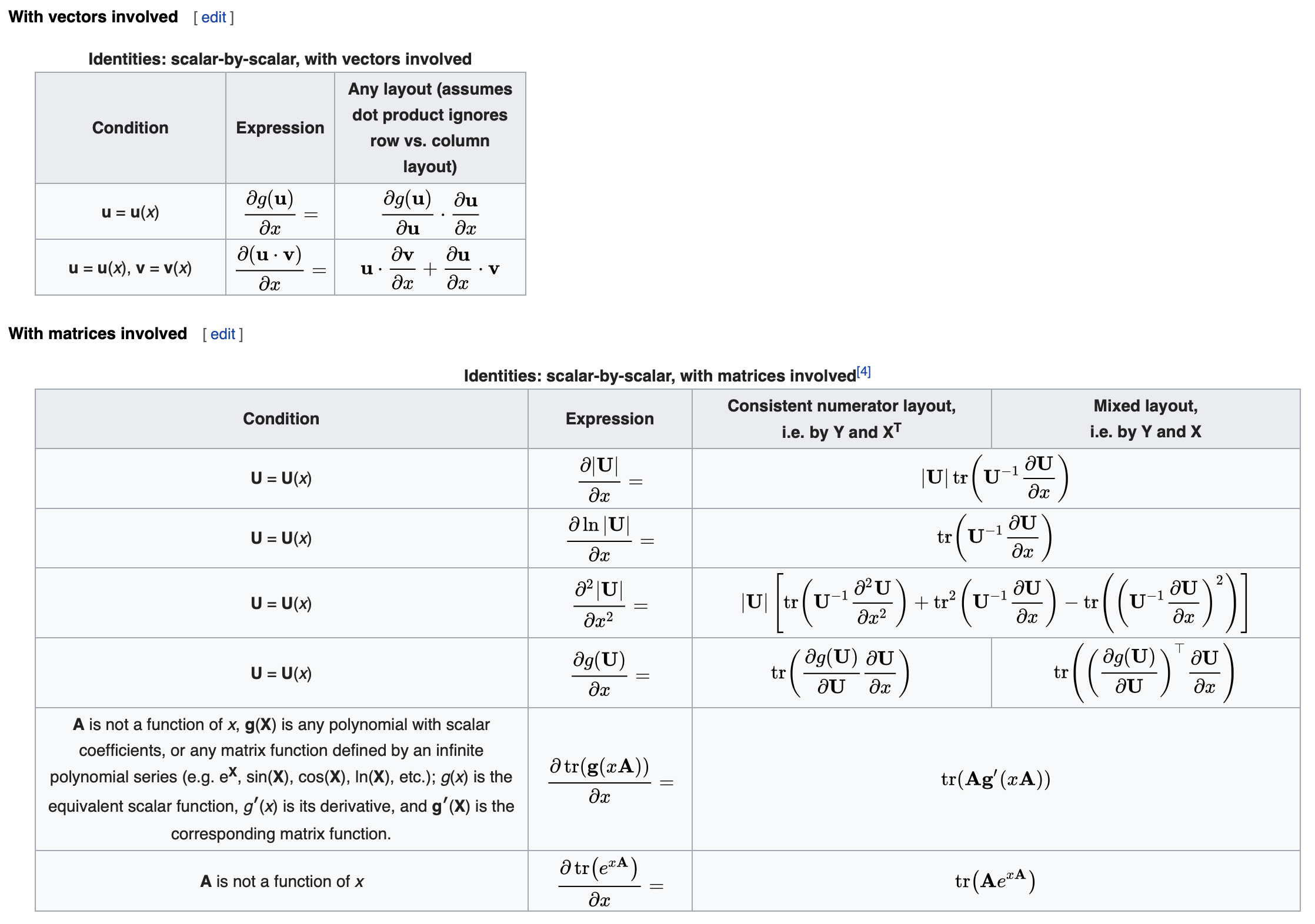
一些恒等式
常用等式
\[||\boldsymbol{X}||^2 = \mathrm{tr}(\boldsymbol{X}^\mathrm{T}\cdot\boldsymbol{X}) = \mathrm{tr}(\boldsymbol{X}\cdot\boldsymbol{X}^\mathrm{T})\] \[\mathrm{tr(\boldsymbol{A}\boldsymbol{B}\boldsymbol{C}\boldsymbol{D})} = \mathrm{tr(\boldsymbol{B}\boldsymbol{C}\boldsymbol{D}\boldsymbol{A})} = \mathrm{tr(\boldsymbol{C}\boldsymbol{D}\boldsymbol{A}\boldsymbol{B})} = \mathrm{tr(\boldsymbol{D}\boldsymbol{A}\boldsymbol{B}\boldsymbol{C})}\]转置
由上述的向量、矩阵的导数定义,易知:
\[\frac{\partial{y^\mathrm{T}}}{\partial{x}} = \frac{\partial{y}}{\partial{x^\mathrm{T}}} = (\frac{\partial{y}}{\partial{x}})^{\mathrm{T}}\]其中$x,y$为满足上述定义的标量、向量或矩阵。
向量对向量求导恒等式
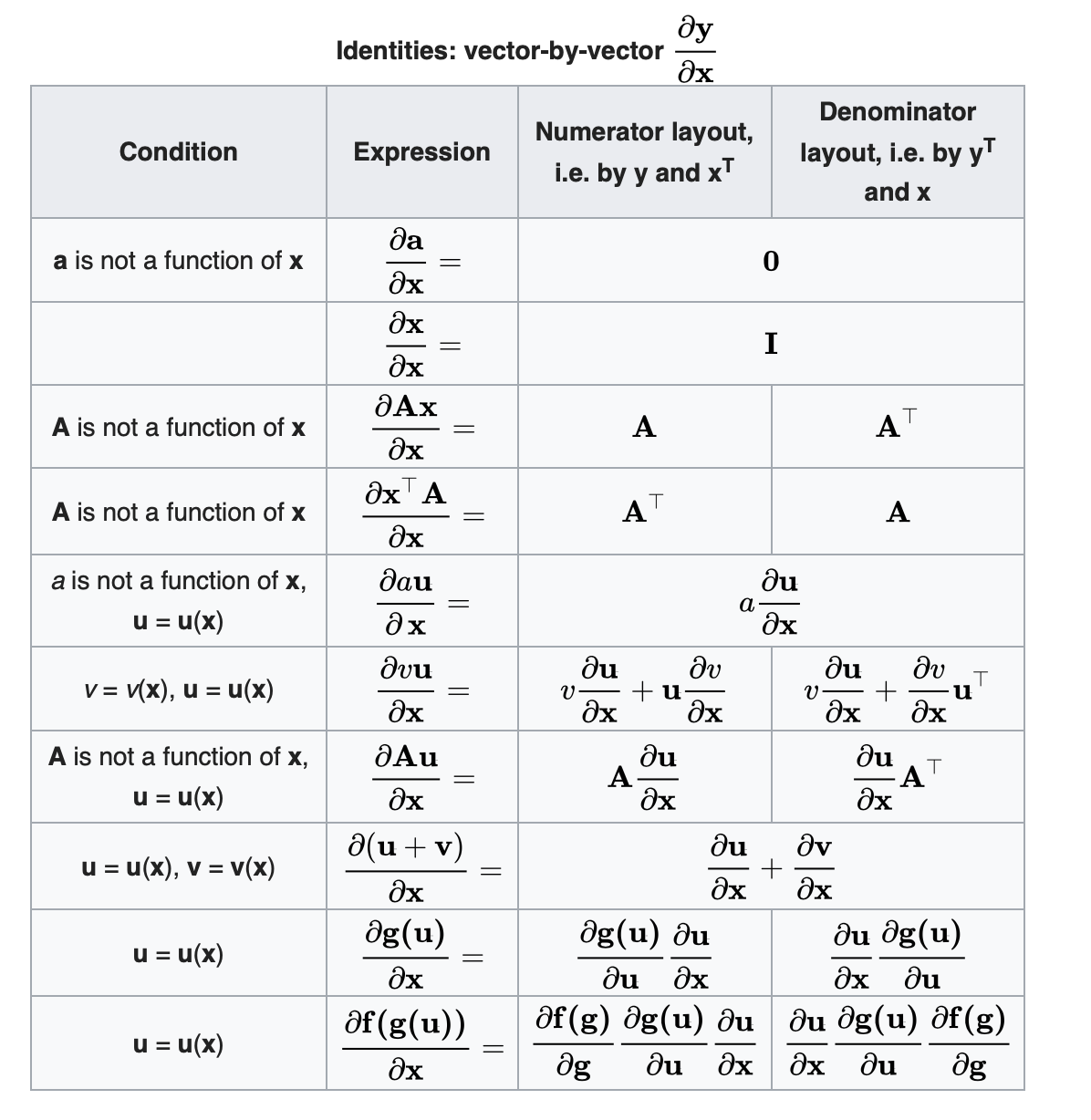
根据上面的定义和求导法则,很容易推导上述结果,下面选择一个进行推导证明:
\[\begin{aligned} (\frac{\partial{v\boldsymbol{u}}}{\partial{\boldsymbol{x}}})_{ij} &= \frac{\partial{vu_i}}{\partial{x_j}} \\ &= v\frac{\partial{u_i}}{\partial{x_j}}+\frac{\partial{v}}{\partial{x_j}}u_i \\ & = v\frac{\partial{u_i}}{\partial{x_j}}+u_i\frac{\partial{v}}{\partial{x_j}} \\ &= v(\frac{\partial{\boldsymbol{u}}}{\partial{\boldsymbol{x}}})_{ij} + (\boldsymbol{u}\frac{\partial{v}}{\partial{\boldsymbol{x}}})_{ij}\\ \Rightarrow \frac{\partial{v\boldsymbol{u}}}{\partial{\boldsymbol{x}}} &= v\frac{\partial{\boldsymbol{u}}}{\partial{\boldsymbol{x}}} + \boldsymbol{u}\frac{\partial{v}}{\partial{\boldsymbol{x}}} \\ \end{aligned}\]标量对向量求导恒等式
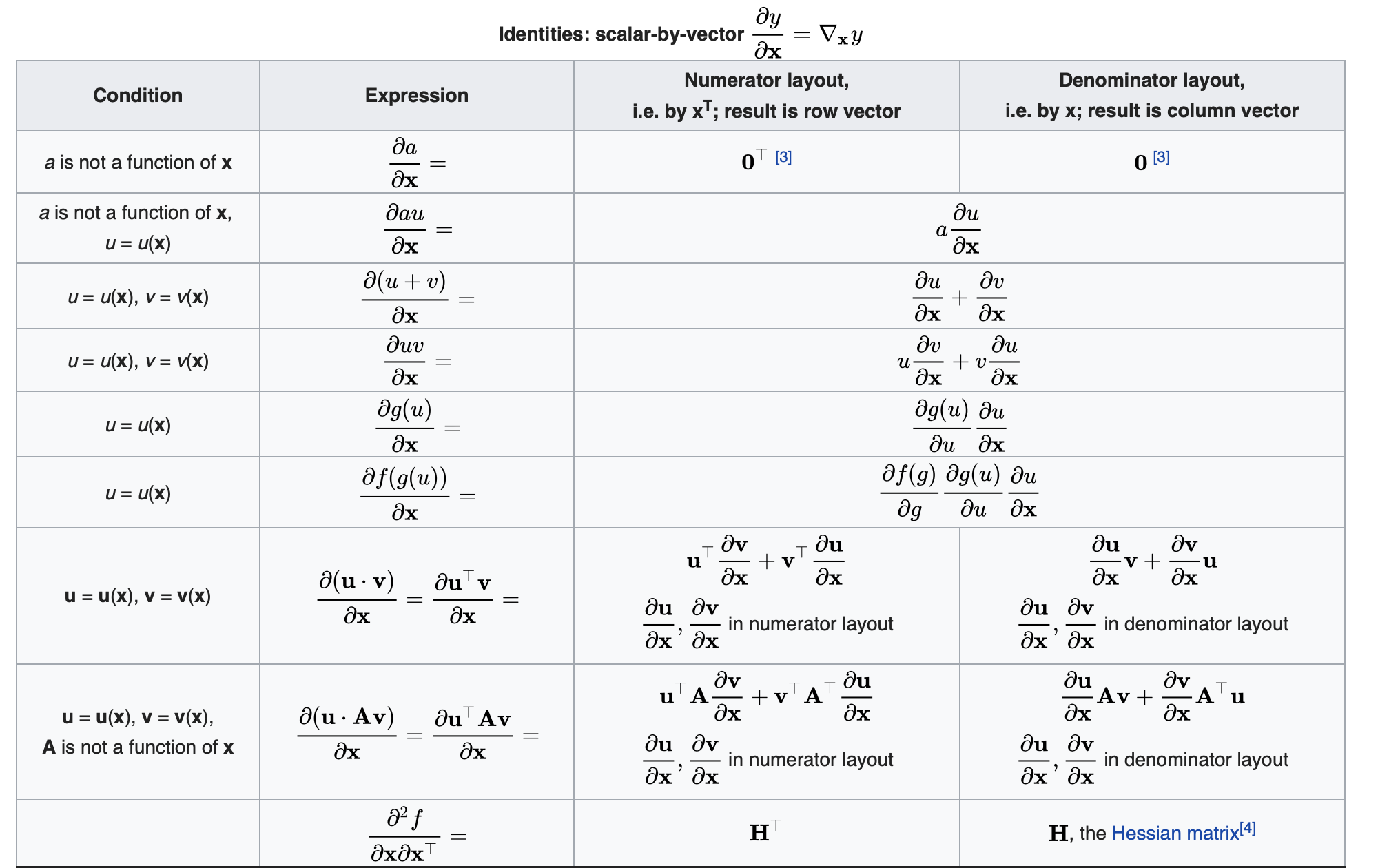

向量对标量求导恒等式
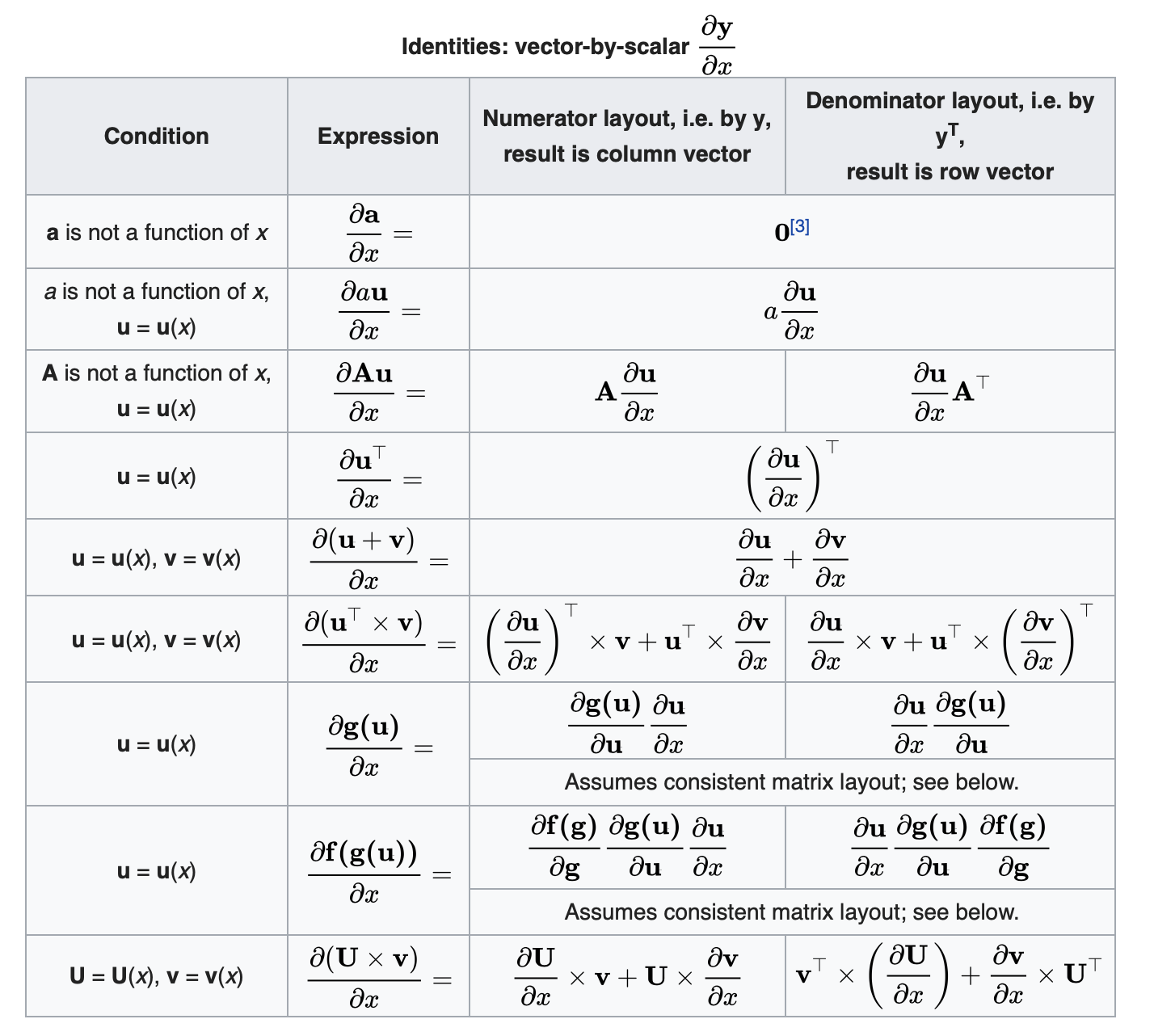
标量对矩阵求导恒等式

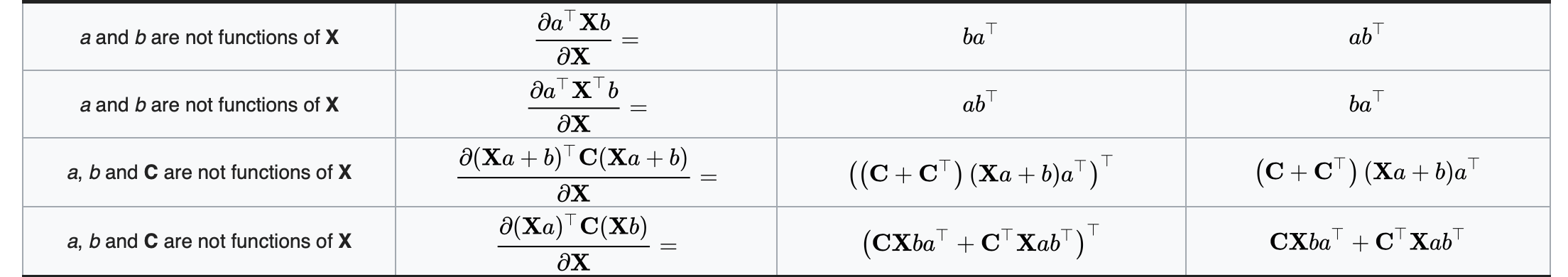
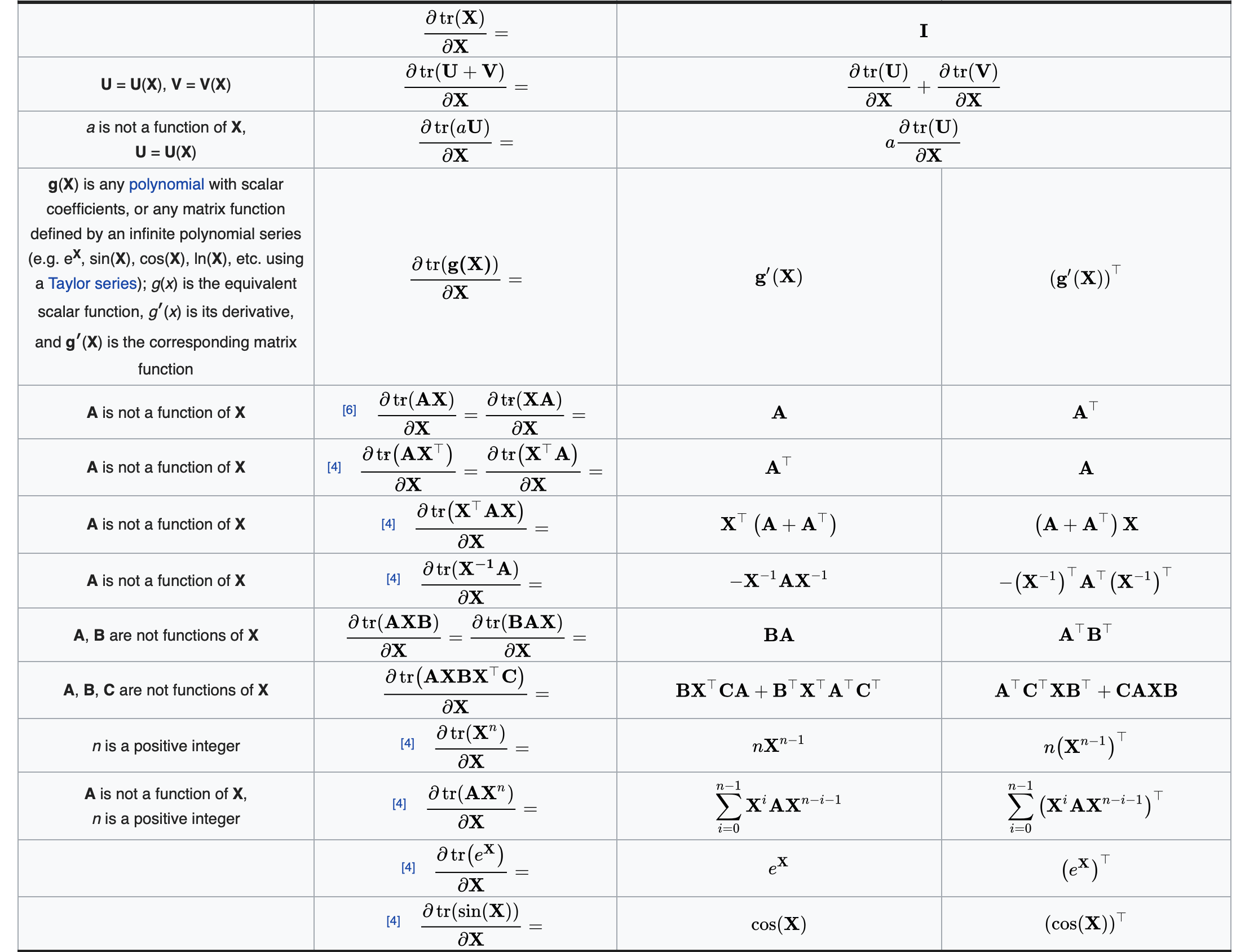
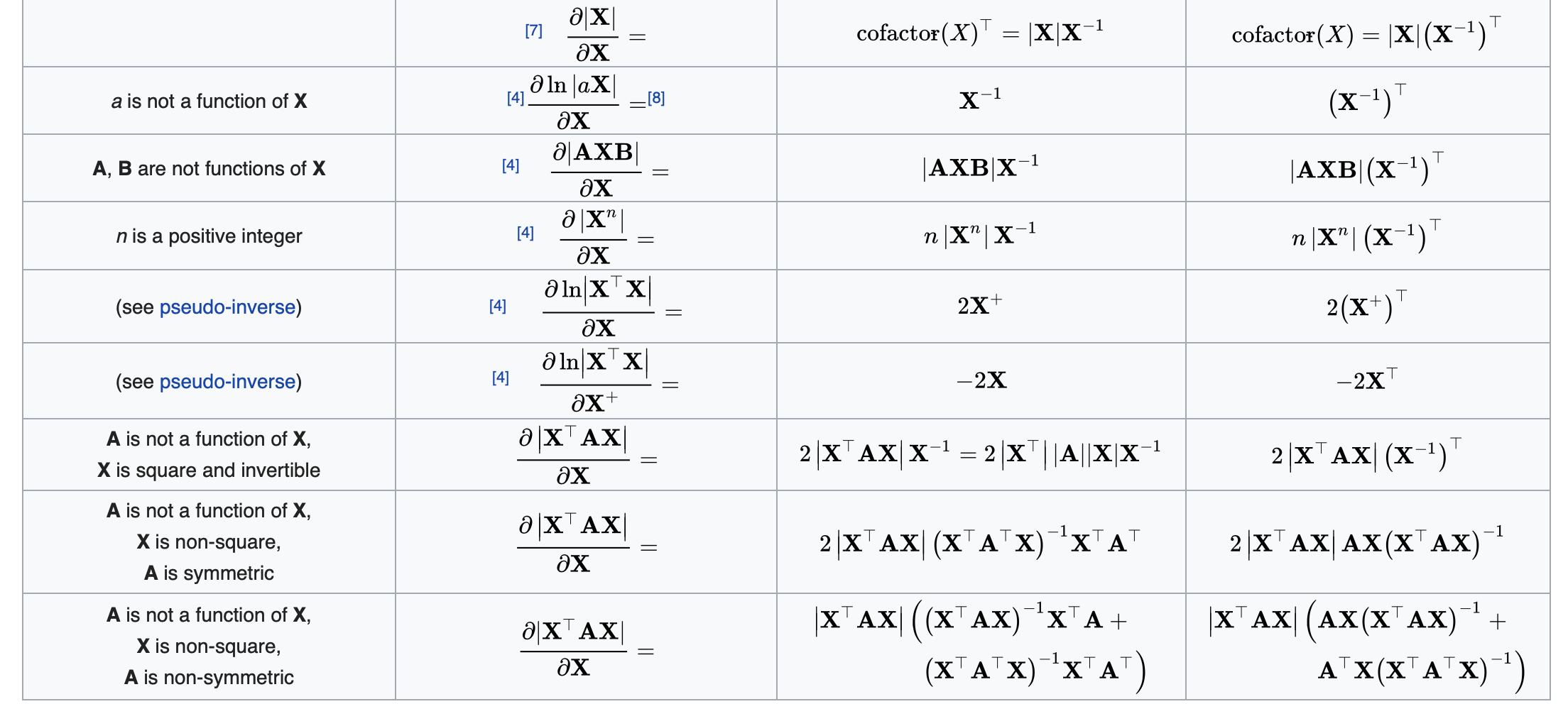
这里选择几个进行证明:
\[\begin{aligned} \frac{\partial{(\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b})^\mathrm{T}\boldsymbol{C}(\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b})}}{\partial{\boldsymbol{X}}} &= \frac{\partial{\mathrm{tr}((\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b})^\mathrm{T}\boldsymbol{C}(\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b}))}}{\partial{\boldsymbol{X}}} \\ & = \frac{\partial{\mathrm{tr}((\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b})^\mathrm{T}\boldsymbol{C}(\boldsymbol{X_1}\boldsymbol{a}+\boldsymbol{b}))}}{\partial{\boldsymbol{X_1}}}+\frac{\partial{\mathrm{tr}((\boldsymbol{X_2}\boldsymbol{a}+\boldsymbol{b})^\mathrm{T}\boldsymbol{C}(\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b}))}}{\partial{\boldsymbol{X_2}}}\\ & = \frac{\partial{\mathrm{tr}((\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b})^\mathrm{T}\boldsymbol{C}\boldsymbol{X_1}\boldsymbol{a})}}{\partial{\boldsymbol{X_1}}}+\frac{\partial{\mathrm{tr}((\boldsymbol{X_2}\boldsymbol{a})^\mathrm{T}\boldsymbol{C}(\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b}))}}{\partial{\boldsymbol{X_2}}}\\ &=\boldsymbol{a}(\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b})^\mathrm{T}\boldsymbol{C}+(\boldsymbol{C}(\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b})\boldsymbol{a}^\mathrm{T})^\mathrm{T}\\ &=\boldsymbol{a}(\boldsymbol{X}\boldsymbol{a}+\boldsymbol{b})^\mathrm{T}(\boldsymbol{C}+\boldsymbol{C}^\mathrm{T}) \end{aligned} \\ \blacksquare\] \[\begin{aligned} f = \frac{\partial{\mathrm{tr}(\mathrm{\boldsymbol{X}^{-1}\boldsymbol{A})}}}{\partial{\boldsymbol{X}}} &= \frac{\partial{\mathrm{tr}(\boldsymbol{X}^{-1}\boldsymbol{X}\boldsymbol{X}^{-1}\boldsymbol{A})}}{\partial{\boldsymbol{X}}} \\ &= \frac{\partial{\mathrm{tr}(\boldsymbol{X}^{-1}_1\boldsymbol{X}\boldsymbol{X}^{-1}\boldsymbol{A})}}{\partial{\boldsymbol{X}_1}} +\frac{\partial{\mathrm{tr}(\boldsymbol{X}^{-1}\boldsymbol{X}_2\boldsymbol{X}^{-1}\boldsymbol{A})}}{\partial{\boldsymbol{X}_2}} +\frac{\partial{\mathrm{tr}(\boldsymbol{X}^{-1}\boldsymbol{X}\boldsymbol{X}^{-1}_3\boldsymbol{A})}}{\partial{\boldsymbol{X}}_3} \\ &=f + \boldsymbol{X}^{-1}\boldsymbol{A}\boldsymbol{X}^{-1} + f \\ \Rightarrow f &=-\boldsymbol{X}^{-1}\boldsymbol{A}\boldsymbol{X}^{-1} \end{aligned}\\ \blacksquare\] \[\begin{aligned} |\boldsymbol{X}|\boldsymbol{I} = \mathrm{adj}(\boldsymbol{X})\boldsymbol{X} \Rightarrow &|\boldsymbol{X}| = \sum_{j}\mathrm{adj}(\boldsymbol{X})_{ij}\boldsymbol{X}_{ji} \qquad \forall i \\ \Rightarrow & (\frac{\partial|\boldsymbol{X}|}{\partial{\boldsymbol{X}}})_{ij} = \frac{\partial|\boldsymbol{X}|}{\partial{\boldsymbol{X}}_{ji}} = \mathrm{adj}(\boldsymbol{X})_{ij} \\ \Rightarrow & \frac{\partial|\boldsymbol{X}|}{\partial{\boldsymbol{X}}} = \mathrm{adj}(\boldsymbol{X}) = |\boldsymbol{X}|\boldsymbol{X}^{-1} \end{aligned} \\ \blacksquare\]上面证明过程中用到了伴随矩阵的性质,伴随矩阵的第$i$行对应的是代数余子式的第$i$列,而代数余子式的第$i$列的元素必定去掉了元素$\boldsymbol{X}$的第$i$列,也就是说伴随矩阵的第$i$行元素全部与$\boldsymbol{X}_{ji}$无关。关于伴随矩阵的具体性质可以参见Adjugate matrix。
其他大部分证明过程类似,或者用了类似的思想,这里由于敲公式太累了,也没有这么多时间,就不一一放出证明过程了。
矩阵对标量求导恒等式
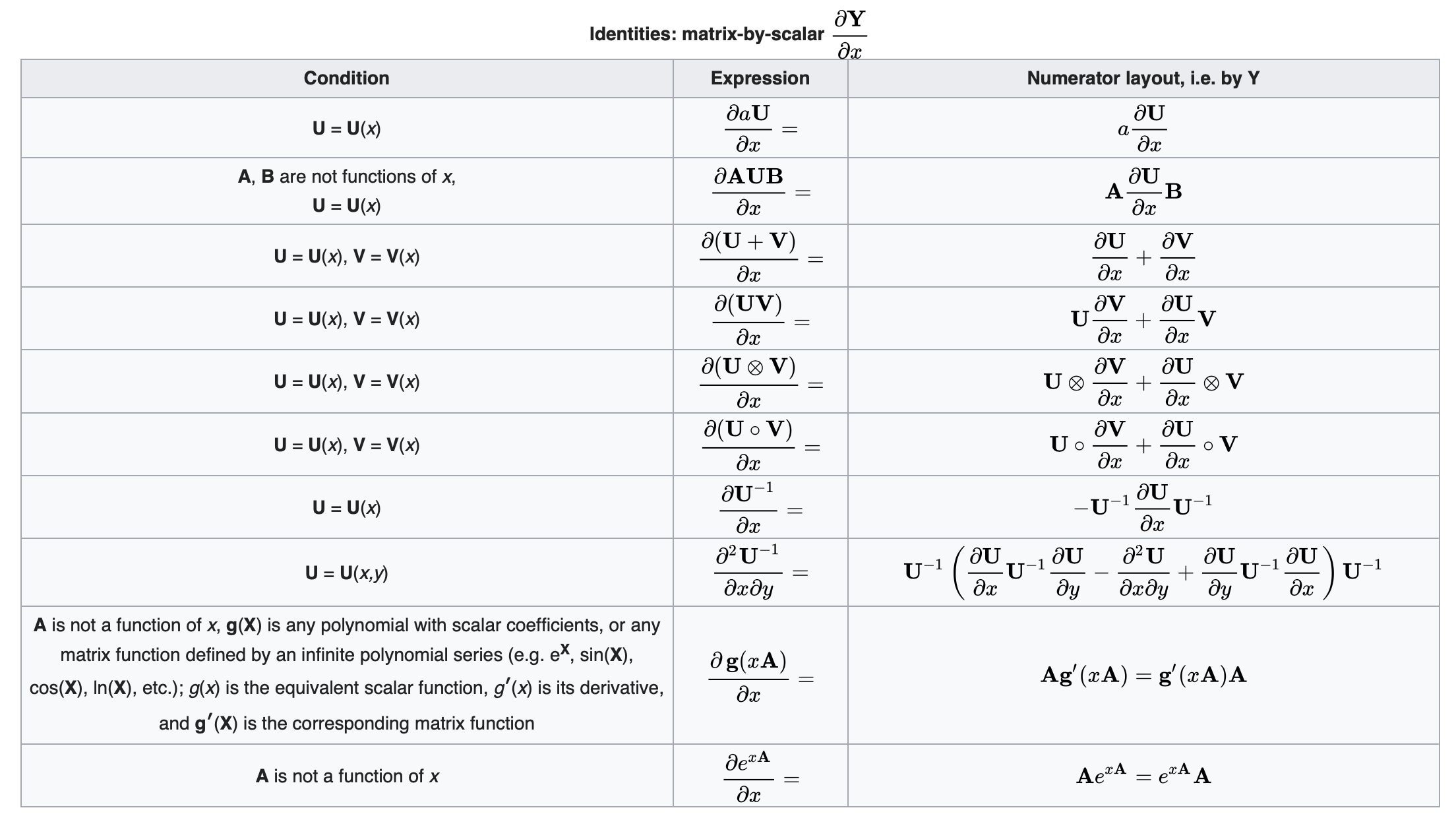
标量对标量求导恒等式