Triplet Loss(FaceNet)
方法:通过CNN将人脸映射到欧式空间的特征向量上,计算不同图片人脸的特征距离。
学习过程如下图所示:
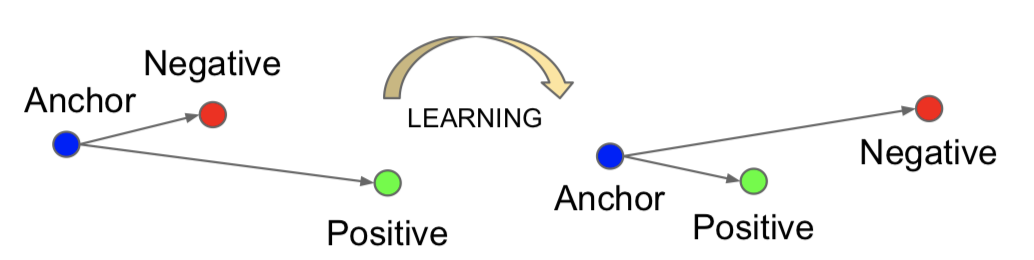
每一次前向传播过程,网络输入的是一个三元组(a,p,n),anchor和positive属于同一个类别,anchor和negative同于不同类别。然后网络训练的目的是使,外加约束margin的情况下,anchor和positive的距离要小雨anchor和negative的距离。
\[||f(x_i^a)-f(x_i^p)||_2^2 + \alpha < ||f(x_i^a)-f(x_i^n)||_2^2\]相应的损失函数如下:
\[\sum_i^N[||f(x_i^a)-f(x_i^p)||_2^2 - ||f(x_i^a)-f(x_i^n)||_2^2+\alpha]_+\]选择三元组方法:
- easy triplets:d(a, n) > d(a, p) + margin,这种情况loss为0,不需要优化
- hard triplets:d(a, n) < d(a, p),即a,p的距离远
- semi-hard triplets:d(a, p) < d(a, n) < d(a, p) + margin,即a, n的间距减去a, p的间距小于预设的margin
在线挖掘策略:
- 原始形式:针对每个anchor依次选择pos,然后选择符合条件的neg
- batch all:选择所有合格的triplet,然后求平均则
- batch hard:选择距离最大的pos样本,选择距离最小的neg样本
Center Loss
Center Loss就是每一个样本到中心的距离的loss,注意中心要更新。
Softmax系列
Softmax loss
其实是softmax操作加上了交叉熵之后的损失
\[L = -\frac{1}{m}\sum_{i=1}^m\log\frac{e^{W_{y_i}^Tx_i+b_{y_i}}}{\sum_{j=1}^ne^{W_j^Tx_i+b_j}}\]W-Norm Softmax
将偏置$b_j$置为0,然后权重和输入的内积用下面式子表示
\[W_j^Tx_i = ||W_j||\cdot||x_i||\cos\theta_j\]再将权重进行$L_2$正则化,使得$||W_j||=1$,则Loss变为
\[L=-\frac{1}{m}\sum_{i=1}^m\log\frac{e^{||x_i||\cos(\theta_{y_i})}}{e^{||x_i||\cos(\theta_{y_i})}+\sum_{j=1,j\neq y_i}^n e^{||x_i||\cos\theta_j}}\]A-Softmax(SphereFace)
由于当$m>1$时,$\cos\theta > \cos m\theta$,将正确分类的角度乘以$m$,loss变为
\[L=-\frac{1}{m}\sum_{i=1}^m\log\frac{e^{||x_i||\cos(m\theta_{y_i})}}{e^{||x_i||\cos(m\theta_{y_i})}+\sum_{j=1,j\neq y_i}^n e^{||x_i||\cos\theta_j}}\]F-Norm SphereFace
将$x_i$进行归一化,同时乘以scale参数$s$,loss变为
\[L=-\frac{1}{m}\sum_{i=1}^m\log\frac{e^{s\cos(m\theta_{y_i})}}{e^{s\cos(m\theta_{y_i})}+\sum_{j=1,j\neq y_i}^n e^{s\cos\theta_j}}\]AM-Softmax(CosinFace)
将正确分类的$\cos\theta$改为$\cos\theta - m$,loss变为
\[L=-\frac{1}{m}\sum_{i=1}^m\log\frac{e^{s(\cos(\theta_{y_i})-m)}}{e^{s(\cos(\theta_{y_i})-m)}+\sum_{j=1,j\neq y_i}^n e^{s\cos\theta_j}}\]additive angular margin loss(ArcFace)
将正确分类的$\cos\theta$改为$\cos(\theta+m)$,由于$\cos\theta > \cos(\theta+m)$,所以增大了分类边界,loss变为
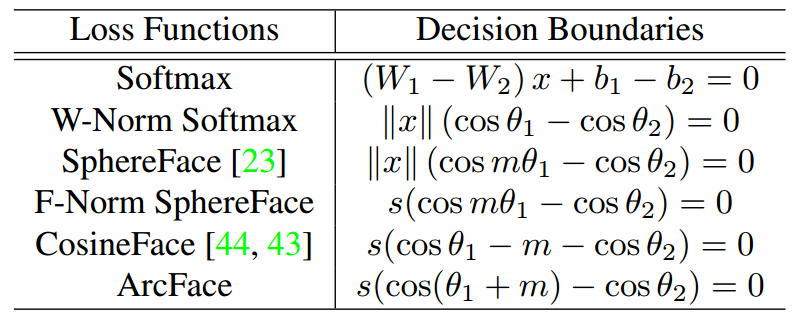
\[L=-\frac{1}{m}\sum_{i=1}^m\log\frac{e^{s\cos(\theta_{y_i}+m)}}{e^{s\cos(\theta_{y_i}+m)}+\sum_{j=1,j\neq y_i}^n e^{s\cos\theta_j}}\]分类边界
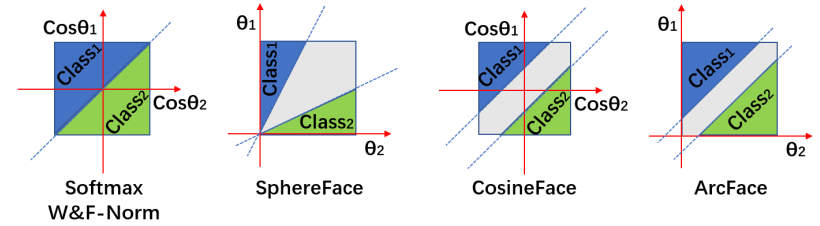
分类边界如下所示: