分类评价指标
这里只讨论2分类问题,不失一般性地、分别为正类和负类。
混淆矩阵(Confusion Matrix)
根据实际类别和预测类别的不同取值,可以构成混淆矩阵
| 实际\预测 | 正 | 负 |
|---|---|---|
| 正 | TP | FN |
| 负 | FP | TN |
以目标检测举例:
- TP:实际有目标,检测出目标
- FN:实际有目标,没有检测出目标
- FP:实际无目标,检测出目标
- TN:实际无目标,没有检测出目标
准确率(Accuracy)
定义:总样本中正确分类所占的比例(所有样本中,正确判断出有目标和没有目标所占的比例)
\[\text{acc} = \frac{TP+TN}{TP+FN+FP+TN}\]精确率(Precision)
定义:判断为正类中真正类所占的比例(所有检测出目标中,实际有目标所占的比例)
\[\text{P} = \frac{TP}{TP+FP}\]召回率(Recall)
定义:正类中预测为正类所占的比列(所有实际有目标的样本中,被检测出有目标所占的比例)
\[\text{R} = \frac{TP}{TP+FN}\]调和平均F值
F值为精确率和召回率的调和平均
\[F_{\beta} = \frac{(1+{\beta}^2)\cdot P\cdot R}{\beta^2\cdot P + R}\]特别地,当$\beta=1$时,$F_1$值表示为
\[\begin{aligned} \frac{2}{F_1} &= \frac{1}{P} + \frac{1}{R} \\ F_1 &= \frac{2\cdot P\cdot R}{P+R} \end{aligned}\]PR曲线
一般情况下,无法同时获得高的精确率和召回率。根据不同的阈值,可以得到不同的精确率和召回率。PR曲线以召回率为横坐标,精确率为纵坐标,如下形式:
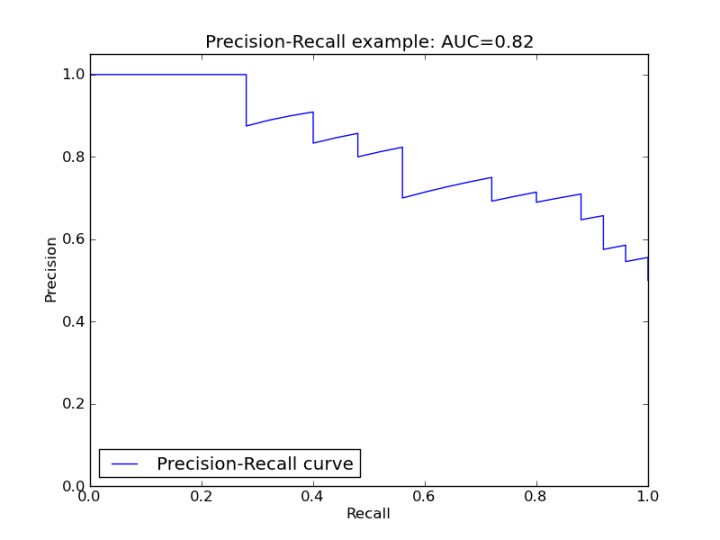
ROC曲线
真正率(TPR,True Positive Rate)定义:实际正类中,预测正类所占的比例,其实就是召回率R
假正率(FPR,False Positive Rata)定义:实际负类中,预测为正类所占的比例。
\[\begin{aligned} TPR &= \frac{TP}{TP+FN} \\ FPR &= \frac{FP}{FP+TN} \end{aligned}\]以FPR为横坐标,TPR为纵坐标,所绘制的曲线即为ROC曲线,如下图所示:
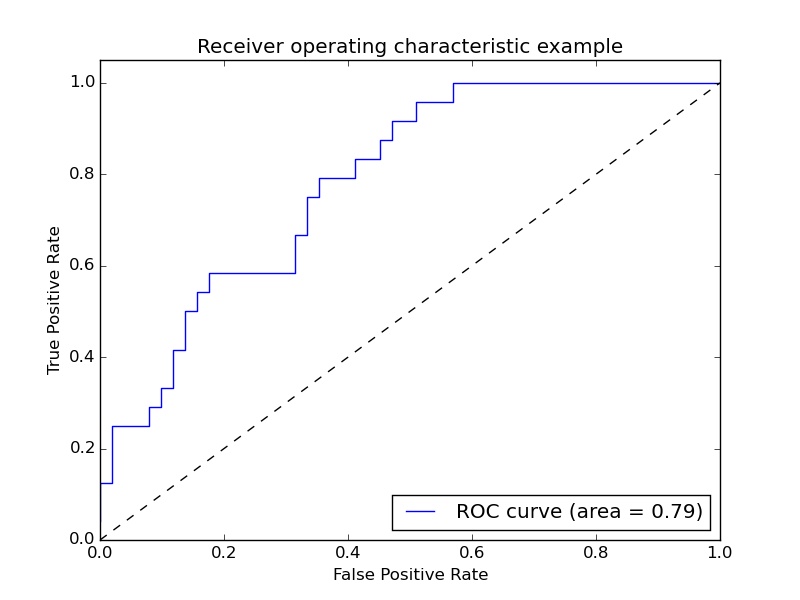
AUC是Area under curve的首字母缩写,即为ROC曲线下面积。
AP和MAP
AP(Average Precision)其实就是PR曲线下面积,mAP(mean Average Precision)为所有类的AP的平均值。
回归评价指标
MSE
MSE(Mean Squared Error)中文均方误差,公式如下:
\[MSE = \frac{1}{m}\sum_{i=1}^{m}(y_i-\hat{y_i})^2\]一般情况也为回归的损失函数。
RMSE
RMSE(Root Mean Squared Error)中文均方根误差,公式如下:
\[RMSE = \sqrt{MSE}\]MAE
MAE(Mean Absolute Error)中文平均绝对误差,公式如下:
\[MAE = \frac{1}{m}\sum_{i=1}^{m}|y_i-\hat{y_i}|\]其实说到底, MAE和MSE就是L1和L2范数的区别。
R-Squared
MSE和MAE之类的不能将正确率归一化为0~1之间,而R-Squared可以,具体公式如下:
\[R^2 = 1-\frac{SS_{residual}}{SS_{total}} = 1-\frac{\sum(y_i-\hat{y})^2}{\sum(y_i-\bar{y})^2} = 1-\frac{MSE(y, \hat{y})}{Var(y)}\]其中MSE为均方误差,Var为方差。

